* 이 글은 김성훈 교수님의 모두를 위한 머신러닝 강의를 수강한 뒤 그 내용을 복습하고자 작성한 글입니다. *
- 이전 게시글 링크 -
- 1 - 머신러닝의 개념 : saltyzun.tistory.com/4
- 2 - 선형회귀(Linear Regression) : saltyzun.tistory.com/7
- 3 - 다중선형회귀(Multiple Linear Regression) : saltyzun.tistory.com/10
4. 로지스틱회귀(Logistic Regression)
(1) Concept of Logistic Regression
앞서, 독립변수와 종속변수 간의 관계를 좌표상에 그렸을 때, 그 형태를 직선으로 나타낼 수 있는 선형회귀에 대해 살펴보았다. 그런데 현실에서는 직선으로 표현하기 어려운 관계 역시 존재한다. 예를 들어, 공부 시간에 따른 시험의 합격/불합격 여부 예측은 기존의 선형 모델을 사용하기 어렵다. 아래의 그래프를 보면 알 수 있듯, 좌표의 형태가 직선으로 표현되기 어렵기 때문이다. 이 때 사용될 수 있는 것이 바로 로지스틱 회귀이다.

(2) Hypothesis(Cocept of Sigmoid Function)
위와 같은 상황에서 두 변수(학습시간과 합격여부) 간의 관계를 잘 표현해주기 위해서는 아래와 같이 S자 형태의 그래프가 그려지는 함수가 필요하다.

이처럼 S자 형태로 그래프가 그려지는 함수를 시그모이드 함수라 하는데, 로지스틱회귀에서는 이와 같은 시그모이드 함수를 가설함수로 사용해 주어진 입력에 대한 결과 값을 예측한다.

여기서 a는 그래프의 경사도, b는 그래프의 좌우 이동을 의미하는데, 선형회귀에서 직선함수의 기울기와 y 절편 값에 따라 오차가 발생했듯, 로지스틱회귀에서도 시그모이드 함수의 a와 b 값의 변화에 따라 오차가 발생하게 된다. 따라서 이에 따른 오차함수를 정의해야 한다.
(3) Cost Function
앞선 장들에서 살펴본 바와 같이 회귀모델이 좋은 성능을 발휘하기 위해서는 실제 값과 가설을 통해 예측한 값의 오차가 작아지게끔 가설함수의 기울기와 절편을 수정해야할 필요가 있다. 그러기 위해서는 적절한 오차함수가 필요한데 로지스틱회귀 모델의 오차함수는 다음과 같이 정의할 수 있다.
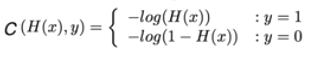
(4) 마무리
지금까지 머신러닝의 기본이 되는 로지스틱회귀에 대해 알아보았다. 로지스틱 회귀는 참/거짓 분류와 결과 값이 0 또는 1 이 되는 상황에서 사용되는 모델이며, 직선을 Hypothesis(가설함수)로 가지는 선형회귀와 달리 S자 형태의 곡선(Sigmoid function)을 Hypothesis로 가진다. 이 때 모델의 성능을 평가하고 개선하기 위해 선형회귀와는 다른 별도의 Cost function(비용함수)이 필요하며, 그 Cost function은 로그 함수로 정의된다.
'AI, ML' 카테고리의 다른 글
| [NLP/Text classification] 데이콘(Dacon) 텍스트 분류 대회 도전기 (0) | 2021.10.02 |
|---|---|
| [AI] 딥러닝(기본) - 3 - 다중선형회귀(Multiple Linear Regression) (0) | 2020.10.30 |
| [AI] 딥러닝(기본) - 2 - 선형회귀(Linear Regression) (0) | 2020.10.19 |
| [AI] 딥러닝(기본) - 1 - 머신러닝의 개념 (0) | 2020.09.13 |




댓글