[AI] 딥러닝(기본) - 2 - 선형회귀(Linear Regression)

* 이 글은 김성훈 교수님의 모두를 위한 머신러닝 강의를 수강한 뒤  그 내용을 복습하고자 작성한 글입니다. *

 

- 앞 장의 내용 요약 - 

 

학습의 종류에는 지도학습과 비지도학습이 있으며, 그 중 지도학습에는 회귀와 분류가 있음을 살펴보았다. 이번 글에서는 지도학습 중 회귀(Regression)를 보다 자세히 다뤄보고자 한다. 

---

2. 선형회귀(Linear Regression)

---

(1) Concept of [Linear Regression]

선형회귀는 머신러닝 분야에서 주로 사용되는 알고리즘 중 하나로, 데이터의 분포를 가장 잘 설명할 수 있는 가설(직선함수)을 찾아내는 알고리즘이다. 선형회귀는 주어진 종속 변수와 독립 변수 사이의 관계를 학습해 데이터를 예측할 수 있게 해준다. 

 

예를 들어, 어떤 학급 아이들의 공부시간과 시험성적 데이터를 가지고 있다고 해보자.

[표]  학생별 공부시간과 시험성적

 

이 데이터를 좌표상에 나타내보면 아래와 같을 것이다.

[그래프] 학생별 공부시간에 따른 시험성적 좌표

 

그렇다면 어떤 학생이 있고, 그 학생이 공부를 5시간 정도 했다고 했을 때 그 학생의 점수는 과연 몇점 정도로 예상해볼 수 있을까? 

 

이 때 필요한 것이 선형회귀분석(Linear Regression)이다. 

---

(2) Concept of [Hypothesis / Cost function]

[ Hypothesis ] 

 

먼저, 앞서 작성한 표의 변수간 관계를 잘 설명할 수 있는 직선을 찾아야 한다. 여기서는 Hypothesis H(x)가 그 직선이 된다. 그림으로 예를 들면 아래와 같다.

Hypothesis

 

그리고 이러한 Hypothesis는 기울기를 나타내는 W와 절편 값인 b 에 따라 다양하게 그려질 수 있다. 

 

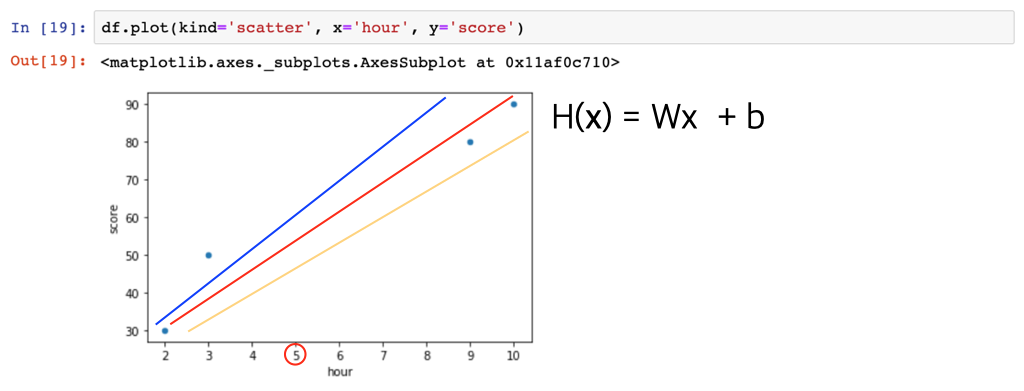
그렇다면, 과연 이들중 어떤 Hypothesis가 주어진 데이터 X(hour) 와 Y(score) 간의 관계를 잘 나타낸  것일까?

 

다음에 이어지는 Cost function(비용함수)을 통해  우리가 찾은 특정 W, b 값이 얼마나 실제 값을 잘 예측하는지 계산해보자.

 

[ Cost function ]

 

우리가 찾은 특정 가설 H(x)가 얼마나 좋은 가설인지 어떻게 계량하여 나타낼 수 있을까?

 

먼저 가설을 통해 예측한 값과 실제 값 간의 차이를 구한 뒤에 여러가설들 중 이 차이값이 가장 작은 가설이 좋은 가설일 것이다. 다시 말해, Linear Regression에서 Cost는 가설 H(x)에 따라 예측된 Y' 값과 실제 Y값 간 의 거리라고 할 수 있으며, 이 Cost 값이 가장 작은 가설이 좋은 가설이다.

 

Cost의 개념을 그림으로 살펴보면 다음과 같다.

Linear Regression Cost

 

m 개의 데이터셋이 주어졌을 때 H(x)의 W,b 값에 따라 Cost가 변하는 Cost function을 아래와 같이 정의할 수 있다. 이 때, Cost function은 각 학습데이터에 대해 가설 H(x)가 예측한 값(y')과 실제 값(y)의 차이를 제곱한 값의 평균이다.

 

Linear Regression Const function

 

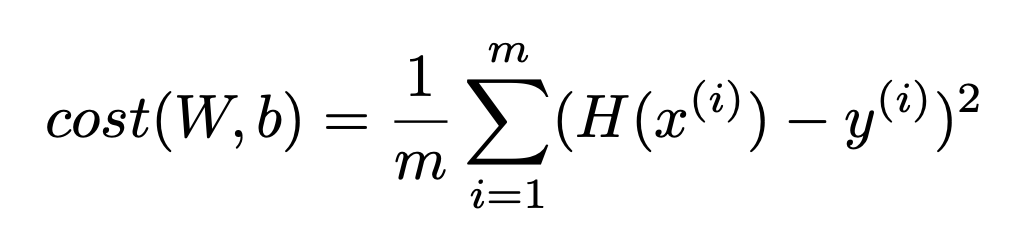
그리고 이러한 Cost function은 아래와 같은 이차함수 형태의 그래프로 나타낼 수 있다.

---

(4) How to minimize cost

이제 마지막으로 남은 문제는 어떻게 하면 Cost function 그래프 상에서 cost가 최소가 되는 W 값을 찾을 수 있는지이다.

 

아이디어는 의외로 매우 간단하다.

 

  1) 임의의 W 값을 설정하고 조금씩 W, b 값을 바꿔가며 cost 값을 줄여간다.

  2) W, b를 바꿀때마다 Gradient에 따라 cost를 줄일 수 있는 방향으로 움직인다.

  3) local minimum 으로 수렴할 때까지 위 과정을 반복한다.

 

How to change the parameter of cost function

 

Linear Regression에서는 위와 같이 최소 cost를 찾는 알고리즘을 경사하강법(Gradient Descent Algorithm) 이라고 하며, 이는 아래와 같이 정의할 수 있다.

Gradient Descent Algorithm

---

(5) 마무리

지금까지 가장 널리 알려진 지도학습 분야인 Linear Regression에 대해 살펴보았다.

 

상관관계가 있는 데이터셋이 주어졌을 때 Linear Regression은 학습을 통해 데이터를 예측할 수 있게끔 해준다. 이 때, 정확한 예측을 하기 위해 Cost(W,b)가 최소가 되는 W 와 b 를 가진 Hypothesis를 찾아내야 하며, Minimum cost를 찾기 위해 경사하강법(Gradient Descendent Algorithm)을 이용할 수 있다.

 

다음글에서는 여러개의 입력값(feature)가 주어지는 Multivariable Linear Regression에 대해 알아보자.