이번 글에서는 컴퓨터 프로그래밍에서 자주 사용되는 자료구조 중 하나인 이진 트리에 관한 내용을 정리해보고자 한다.
1. 이진 트리의 정의 및 성질
먼저, 이진 트리(binary tree)는 공백이거나 루트(root)와 왼쪽 서브 트리, 오른쪽 서브 트리라고 하는 2개의 분리된 이진 트리로 구성된 노드의 유한 집합이다. 이진 트리와 일반적인 트리의 주요한 차이점은 다음과 같다.
- 일반 트리의 경우 0개의 노드를 가질 수 없으나, 공백 이진 트리는 존재함
- 일반 트리는 자식의 순서를 구분하지 않으나, 이진 트리는 왼쪽 자식과 오른쪽 자식을 구별함
또한, 이진 트리는 노드의 수와 관련하여 다음과 같은 성질을 갖는다.
- 레벨 i 에서의 최대 노드 수는 2^(i -1) → 예) 레벨 3에서 최대 노드의 수는 4개
- 깊이가 k인 이진 트리의 최대 노드 수는 2^k -1 → 예) 깊이가 3인 이진 트리의 최대 노드 수는 7개
- n0 = n2 + 1 (리프 노드의 수 = 자식 노드가 2개인 노드의 수 + 1)
2. 포화 이진 트리와 완전 이진 트리
- 포화 이진 트리 : 깊이가 k 이고 노드의 수가 2^k-1(k≥0)인 이진 트리
- 완전 이진 트리 : 포화 이진 트리의 리프들을 오른쪽부터 제거하여 얻어진 트리
3. 이진 트리의 표현
이진 트리는 두 가지 방법으로 표현될 수 있다. 각각의 장단점을 고려해 상황에 맞춰 적합한 방식을 택하면 된다.
- 배열 표현
- i가 1이 아니면 parent(i)는 [i/2]에 위치한다. 만약, i가 1이면 i는 루트이므로 부모가 없다.
- 2i ≤ n 이면 leftChild(i)는 2i 위치에 있다. 만일 2i > n 이면 i 는 왼쪽 자식이 없다
- 2i+1 ≤ n 이면 rightChild(i)는 2i+1 위치에 있다. 만일 2i+1 > n 이면 i 는 오른쪽 자식이다.

배열을 이용해 이진 트리를 표현하는 경우, 완전 이진 트리일 때 이상적 표현이 가능하지만 편향된 트리(skewed tree)인 경우 공간의 낭비가 발생한다. 또한 트리의 중간에 노드를 삽입하거나 삭제하는 경우 노드의 레벨이 변경됨에 따라 위치 변경이 일어나게 된다. 이러한 문제를 극복하기 위해 연결 표현을 사용할 수 있다.
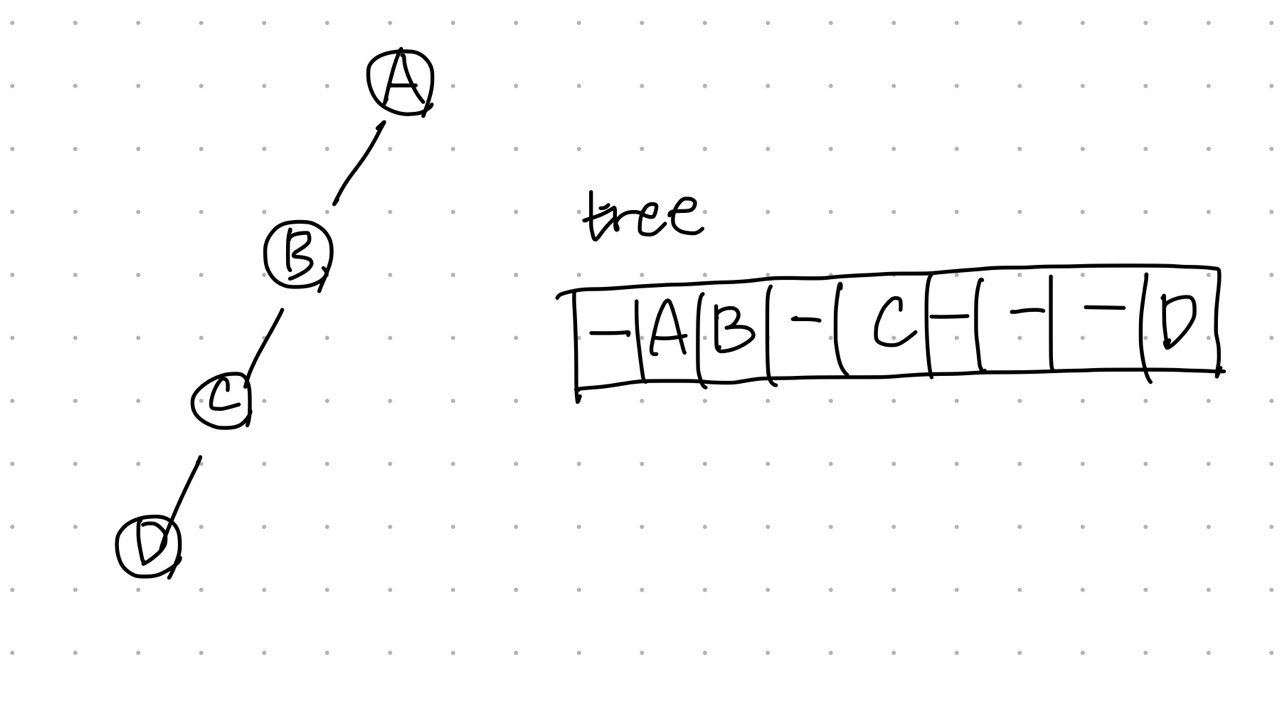
- 연결 표현
- 각 노드를 leftChild, data, rightChild를 가지고 있는 구조체로 만들어 표현한다.
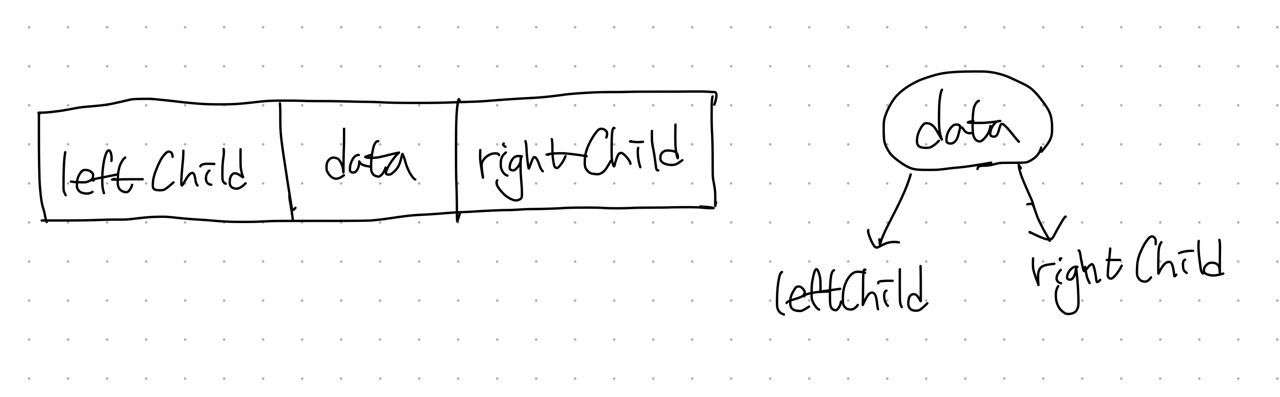
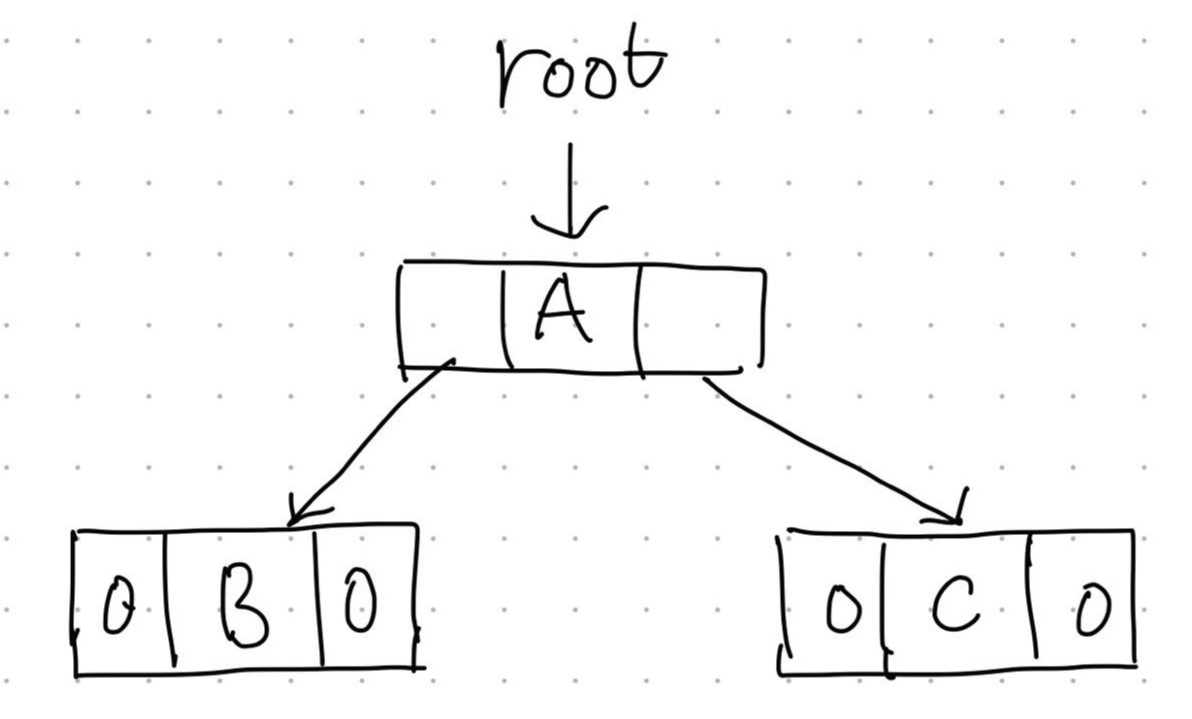
연결 표현을 사용함으로써, 공간의 낭비를 최소화하고, 삽입 삭제 시 비용이 발생하는 순차 표현의 문제를 해소할 수 있다. 그러나 부모 노드 파악이 어렵다는 단점도 존재한다. 이를 해결하기 위해 data, leftChild, rightChild에 더해 4번째 필드 값으로 parent를 추가할 수 있다.
4. 이진 트리 순회
이진 트리 순회에는 세 가지 방법이 있으며, 각종 시험 혹은 면접 등에서 자주 묻는 부분이므로 알아두면 좋다.
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def inorder(node): # Binary tree 중위순회
if node:
inorder(node.left)
print(node.data)
inorder(node.right)
def preorder(node): # Binary tree 전위순회
if node:
print(node.data)
preorder(node.left)
preorder(node.right)
def postorder(node): # Binary tree 후위순회
if node:
postorder(node.left)
postorder(node.right)
postorder(node.data)
'Web Development > CS Basic' 카테고리의 다른 글
| [자료구조] 깊이 우선 탐색(DFS, Depth First Search) 이해 및 Python 구현 - CS면접 대비 (0) | 2021.12.23 |
|---|---|
| [자료구조] AVL Tree(AVL 트리) - CS면접 대비 (0) | 2021.12.07 |
| [자료구조] BST(Binary Search Tree) 이진 탐색 트리 - CS면접 대비 (0) | 2021.12.02 |
| [자료구조] Binary Heap(히프)와 Priority Queue(우선순위 큐) - CS면접 대비 (0) | 2021.11.30 |




댓글