그래프 G의 한 정점 v 가 주어졌을 때, v에 연결된 모든 정점들을 방문하는 방법으로 깊이우선탐색(DFS)과 너비우선탐색(BFS)가 있다. 이 글에서는 깊이우선탐색(DFS)에 대해 정리해보고자 한다.
깊이 우선 탐색(DFS, Depth First Search)
[1] Graph의 정의
먼저, 깊이 우선 탐색은 그래프 자료구조를 탐색하기 위한 방법이자 그래프 자료구조의 대표적인 연산이다. 따라서 그래프 자료구조의 정의부터 살펴보자. 다소 딱딱하게 느껴지겠지만, 전공서적에 있는 정의를 그대로 가져와 써보면 아래와 같다.
그래프 G는 두개의 집합 V와 E로 구성되며 다음과 같이 정의할 수 있다.
- V(G) : 공집합이 아닌 정점(Vertice)의 유한 집합.
- E(G) : 정점 쌍들의 집합으로, 이러한 쌍을 간선(Edge)라고 한다.
- 임의의 그래프는 G=(V, E)로 표기할 수 있다.
다음으로, 위에서 정의한 그래프는 다음과 같은 제약조건을 가진다.
- 임의의 정점 v에서 자신으로 이어지는 간선을 가질 수 없다(self-edge, self-loop을 허용하지 않는다)
- 같은 간선을 중복해서 가질 수 없다(multigraph를 허용하지 않는다)
끝으로, 각종 시험 혹은 면접 등에서 그래프 자료구조에 대해 물어볼 때 함께 언급되는 개념 혹은 용어를 정리하면 다음과 같다.
- 완전그래프(Complete Graph) : N개의 정점을 가지는 무방향 그래프의 최대 간선 수는 N(N-1)/2 이다. 이 때, N개의 정점과 N(N-1)/2 개의 간선을 가지는 그래프를 완전 그래프라 한다.
- 인접하다(Adjecent) : (u, v) 가 E(G)의 한 간선이라면 u와 v는 인접한다고 표현한다.
- 사이클(Cycle) : 한 경로상에서 처음과 마지막을 제외한 모든 정점들이 서로 다를 때, 이를 단순경로(Simple path)라 하고, 이 중에서 처음과 마지막 정점이 같은 단순경로를 사이클이라 한다.
[2] 깊이 우선 탐색 (DFS)
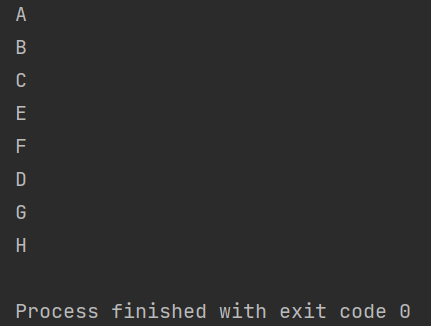
코드를 살펴보기에 앞서, 깊이 우선 탐색의 예를 그림을 통해 파악해보자. 아래와 같은 그래프가 주어졌을 때 [A-B-C-E-F-D-G-H] 순서로 정점들을 방문하는 알고리즘이 깊이 우선 탐색이다.

이러한 깊이 우선 탐색 알고리즘을 글로 써보면 아래와 같다.
- 출발 정점 v 를 방문한다.
- v에 인접하면서 아직 방문하지 않은 정점 w를 선택해 w를 시작점으로 하는 깊이우선탐색을 다시 시작한다. (이 때, w가 이미 방문한 정점인 경우 무시하고, 아직 방문하지 않은 경우 방문한 후 스택에 삽입한다.)
- v의 인접리스트에서 현재 위치는 스택에 넣어 기억시킨다. (다시 되돌아오기 위해)
- 스택이 공백이 되면 탐색은 종료된다. (더 이상 방문할 정점이 존재하지 않기 때문에)
DFS 탐색 알고리즘은 그래프에 있는 노드들을 최대 한번씩만 방문하므로 시간복잡도는 O(E) 이며, 만약 G를 인접행렬로 표현한 경우 O(V^2) 이다.
[3] 깊이 우선 탐색 구현
깊이 우선 탐색의 개념을 이해했더라도 막상 구현하고자 한다면 어렵다고 느껴질 수 있다. 따라서 직접 구현해보고자 한다면 다음의 파이썬 코드를 참고하면 된다.
1. 그래프 초기화 (위 그림과 같은 상태임)
graph = dict()
graph['A'] = ['B', 'D']
graph['B'] = ['C', 'E']
graph['C'] = ['']
graph['D'] = ['E', 'G', 'H']
graph['E'] = ['F']
graph['F'] = ['']
graph['G'] = ['H']
graph['H'] = ['']
2. 깊이 우선 탐색
깊이 우선 탐색 구현 시에는 항상 두 개의 리스트를 사용해야 한다는 점을 기억하자. 하나는 해당 정점을 방문했는지 여부를 기록하는 리스트이고, 다른 하나는 정점과 인접한 정점들을 저장하는 스택으로, 이 스택이 공백이 될 때까지 깊이 우선 탐색이 계속된다.
def DFS(graph, start):
if start not in is_visited: # 아직 방문하지 않은 정점인 경우
print(start)
is_visited.append(start) # 방문했음을 기록하고
for vertex in graph.get(start): # 정점과 인접한 다른 정점들에 대해
if vertex:
stack.append(vertex) # 스택에 정점을 추가하고
post = stack.pop() # 스택에서 정점을 꺼낸 뒤
DFS(graph, post) # 스택에서 꺼낸 정점을 시작점으로 다시 탐색
global is_visited
global stack
is_visited = []
stack = []
DFS(graph, 'A')
3. 출력
'Web Development > CS Basic' 카테고리의 다른 글
| [자료구조] AVL Tree(AVL 트리) - CS면접 대비 (0) | 2021.12.07 |
|---|---|
| [자료구조] BST(Binary Search Tree) 이진 탐색 트리 - CS면접 대비 (0) | 2021.12.02 |
| [자료구조] Binary Heap(히프)와 Priority Queue(우선순위 큐) - CS면접 대비 (0) | 2021.11.30 |
| [자료구조] Binary Tree(이진 트리) - CS면접 대비 (0) | 2021.11.16 |




댓글